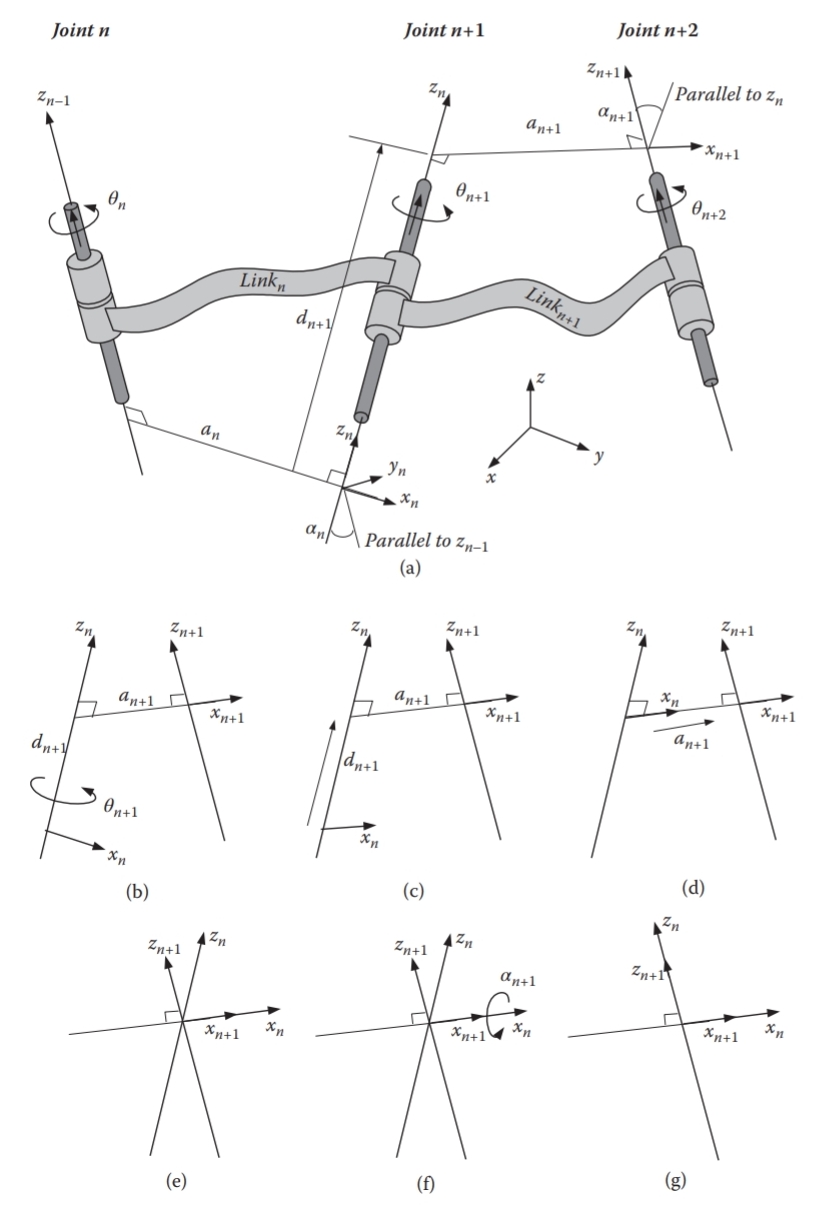
La matriu de transformació D-H \( \mathbf{B} \) s'obté com a producte de quatre matrius bàsiques. A continuació es justifica pas a pas cada element contingut en cadascuna d'aquestes matrius:
La matriu \( \mathbf{R}_z(\theta_n) \) representa la rotació al voltant de l'eix \( z_n \) per un angle \( \theta_n \): \[ \mathbf{R}_z(\theta_n) = \begin{bmatrix} \cos \theta_n & -\sin \theta_n & 0 & 0 \\ \sin \theta_n & \cos \theta_n & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix} \]
Justificació dels elements:
La matriu \( \mathbf{T}_z(d_n) \) representa la translació al llarg de l'eix \( z_n \) per una distància \( d_n \): \[ \mathbf{T}_z(d_n) = \begin{bmatrix} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & d_n \\ 0 & 0 & 0 & 1 \end{bmatrix} \]
Justificació dels elements:
La matriu \( \mathbf{T}_x(a_n) \) representa la translació al llarg de l'eix \( x_n \) per una distància \( a_n \): \[ \mathbf{T}_x(a_n) = \begin{bmatrix} 1 & 0 & 0 & a_n \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix} \]
Justificació dels elements:
La matriu \( \mathbf{R}_x(\alpha_n) \) representa la rotació al voltant de l'eix \( x_n \) per un angle \( \alpha_n \): \[ \mathbf{R}_x(\alpha_n) = \begin{bmatrix} 1 & 0 & 0 & 0 \\ 0 & \cos \alpha_n & -\sin \alpha_n & 0 \\ 0 & \sin \alpha_n & \cos \alpha_n & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix} \]
Justificació dels elements:
La matriu de transformació D-H \( \mathbf{B} \) s'obté multiplicant aquestes quatre matrius: \[ \mathbf{B} = \mathbf{R}_z(\theta_n) \cdot \mathbf{T}_z(d_n) \cdot \mathbf{T}_x(a_n) \cdot \mathbf{R}_x(\alpha_n) \] La qual cosa resulta en: \[ \mathbf{B} = \begin{bmatrix} \cos \theta_n & -\sin \theta_n \cos \alpha_n & \sin \theta_n \sin \alpha_n & a_n \cos \theta_n \\ \sin \theta_n & \cos \theta_n \cos \alpha_n & -\cos \theta_n \sin \alpha_n & a_n \sin \theta_n \\ 0 & \sin \alpha_n & \cos \alpha_n & d_n \\ 0 & 0 & 0 & 1 \end{bmatrix} \]
1. Primera fila:
La primera fila de la matriu és: \[ \begin{bmatrix} \cos \theta_n & -\sin \theta_n \cos \alpha_n & \sin \theta_n \sin \alpha_n & a_n \cos \theta_n \end{bmatrix} \] - \( \cos \theta_n \): És la projecció del cosinus de l'angle de rotació \( \theta_n \) al voltant de l'eix \( z_n \). - \( -\sin \theta_n \cos \alpha_n \): Combina la rotació \( \theta_n \) amb la inclinació \( \alpha_n \) al llarg de l'eix x'. - \( \sin \theta_n \sin \alpha_n \): Representa la component de la rotació \( \theta_n \) i la inclinació \( \alpha_n \) en la direcció z. - \( a_n \cos \theta_n \): És la translació al llarg de l'eix x després de la rotació \( \theta_n \).
2. Segona fila:
La segona fila de la matriu és: \[ \begin{bmatrix} \sin \theta_n & \cos \theta_n \cos \alpha_n & -\cos \theta_n \sin \alpha_n & a_n \sin \theta_n \end{bmatrix} \] - \( \sin \theta_n \): És la projecció del sinus de l'angle de rotació \( \theta_n \) al voltant de l'eix \( z_n \). - \( \cos \theta_n \cos \alpha_n \): Combina la rotació \( \theta_n \) amb la inclinació \( \alpha_n \) al llarg de l'eix x'. - \( -\cos \theta_n \sin \alpha_n \): Representa la component negativa de la rotació \( \theta_n \) i la inclinació \( \alpha_n \) en la direcció z. - \( a_n \sin \theta_n \): És la translació al llarg de l'eix x després de la rotació \( \theta_n \).
3. Tercera fila:
La tercera fila de la matriu és: \[ \begin{bmatrix} 0 & \sin \alpha_n & \cos \alpha_n & d_n \end{bmatrix} \] - \( 0 \): No hi ha cap component de translació o rotació en la direcció x'. - \( \sin \alpha_n \): És la projecció del sinus de l'angle d'inclinació \( \alpha_n \) al llarg de l'eix z. - \( \cos \alpha_n \): Representa la projecció del cosinus de l'angle d'inclinació \( \alpha_n \) al llarg de l'eix z. - \( d_n \): És la distància al llarg de l'eix z després de la translació.
4. Quarta fila:
La quarta fila de la matriu és sempre: \[ \begin{bmatrix} 0 & 0 & 0 & 1 \end{bmatrix} \] Aquesta fila indica que l'última coordenada homogènia es manté constant a 1, la qual cosa és necessària per mantenir la coherència en les transformacions homogràfiques en 3D.
Aquesta matriu \( \mathbf{B} \) es calcula per a cada articulació \( n \) del sistema, i es combina amb altres matrius de transformació per a determinar la posició i orientació finals de l'eina respecte a la base del robot.
La matriu de transformació Denavit-Hartenberg (D-H) és una eina fonamental en la robòtica perquè ofereix una manera sistemàtica i generalitzada de representar la relació entre els diferents enllaços i articulacions d'un robot. Això la fa útil per a una àmplia varietat de robots, independentment de la seva configuració específica. A continuació, es detallen les raons per les quals aquesta matriu és tan versàtil:
La matriu D-H generalitza la manera com es modelen les transformacions entre els enllaços d'un robot, independentment de la seva estructura. Això vol dir que, tant si un robot té una estructura tipus "braç" (amb enllaços articulats en sèrie) com si és un robot "paral·lel", la matriu D-H pot descriure les transformacions necessàries entre les diferents parts del robot.
La notació D-H utilitza quatre paràmetres: angle de gir (\(\theta_n\)), desplaçament (\(d_n\)), longitud de l'enllaç (\(a_n\)) i angle de torsió (\(\alpha_n\)). Aquests quatre paràmetres són suficients per descriure qualsevol configuració d'enllaços en un robot. Com que tots els robots poden ser descrits en termes d'aquests mateixos quatre paràmetres, la matriu D-H es pot aplicar universalment.
La matriu D-H és útil per a robots amb diferents tipus d'articulacions, ja siguin rotacionals o prismàtiques. La seva flexibilitat permet representar tant robots cartesians, cilíndrics, esferoïdals, com robots antropomòrfics (similars a un braç humà), entre altres.
Molts llenguatges de programació i plataformes de control de robots, com ROS (Robot Operating System), utilitzen la notació D-H com a base per a la seva modelització cinemàtica. Això permet que els enginyers i programadors treballin amb una representació estandarditzada que es pot aplicar a qualsevol robot sense necessitat de modificar substancialment el model matemàtic.
Una de les tasques més comunes en robòtica és determinar la posició i orientació de l'extrem d'un robot (la seva "eina") donada una configuració específica de les articulacions. La matriu D-H simplifica aquest procés, ja que permet expressar la posició de l'eina respecte a la base del robot mitjançant una cadena de transformacions simples que es poden resoldre de manera sistemàtica.
Atès que la matriu D-H és tan versàtil, qualsevol canvi en la configuració d'un robot (com afegir un nou enllaç o modificar l'angle d'una articulació) es pot incorporar fàcilment en el model sense necessitat de redissenyar tot el sistema de modelització cinemàtica.
En conclusió, la matriu Denavit-Hartenberg és un model universal i flexible que pot ser aplicat a una gran varietat de robots, permetent una representació compacta i sistemàtica de la cinemàtica de qualsevol manipulador robòtic.