Càlcul de distàncies amb geolocalització

En aquest enllaç de w3Schools pots trobar informació sobre codis JavaScript per geolocalització.

Quan cliquem el botó ens indica que s'ha d'executar onclick, és a dir, quan clico el botó la funció getlocation() que és una funció javascript creada per mi que comprova si el navegador té geolocalitzador emprant if navigator.geolocation tal com pots veure en el codi a continuació per obtenir la posició actual (getCurrentPosition).

var x = document.getElementById("demo");

function getLocation() {
  if (navigator.geolocation) {
    navigator.geolocation.getCurrentPosition(showPosition);
  } else { 
    x.innerHTML = "La geolocalització no està soportada en aquest navegador.";
  }
}

function showPosition(position) {
  x.innerHTML = "Latitud: " + position.coords.latitude + 
  "
Longitud: " + position.coords.longitude;
}

En el següent exemple amb el codi anterior i el portàtil hem mirat la geolocalització de l'aula i la geolocalització de la porta de l'institut que es troba en l'altre extrem del centre i hem trobat:

Longitud de la classe: 1,922328

Latitud de la classe: 41,4750492

Longitud de la porta d'entrada: 1,9216488

Latitud de la porta d'entrada: 41,4752105

Diferència latitud: 0,0001613

Diferència de longitud: 0,0006792 graus

Diferència de latitud en metres: 0,0001613 graus/360x40.075.000 = 17,95 metres

Diferència de longitud en metres: 0,0006792 graus/360x40.075.000 = 75,60 metres

Hem transformat la diferència de latitud i longitud en graus, en metres. Perque 360 graus que és una volta, és igual al seu perímetre de la terra que és 40.075 km que és igual a 40.075.000 metres.

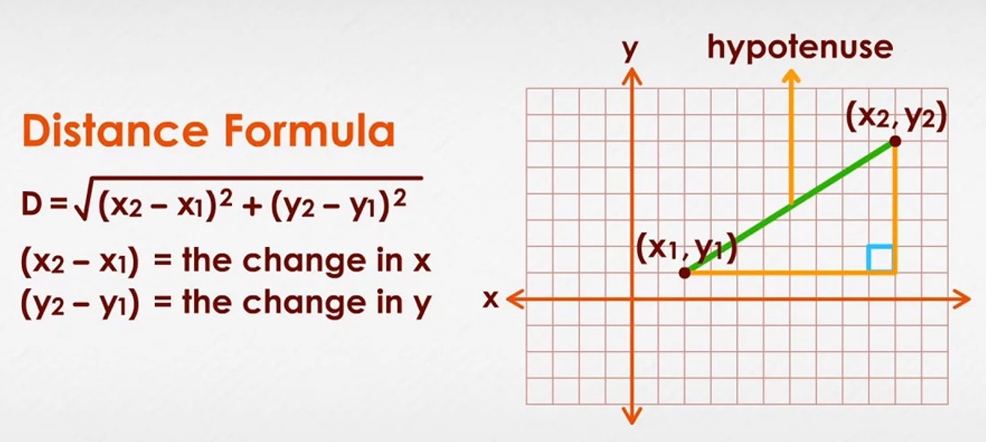
Ara farem Pitàgores amb els números anteriors perquè són la distància del eix X i en el eix Y de la Terra que hem recorregut.

La distància segons pitàgores serà l'arrel quadrada de 17,75 al quadrat més 75,60 al quadrat.

La distància entre la porta de l'institut i la classe és 77,65 metres.

Per fer el càlcul hem de restar la latitud de la classe menys la latitud de la porta. També hem de restar la longitud de la classe de la longitud de la porta. Ara tenim la diferència en graus i hem de passar els graus a metre. Si la terra té 360 graus que són 40.075 km, els graus que calculem seran x quilòmetres. Hem de fer el teorema de Pitàgores amb les dues diferències de latitud i longitud

Euclidian distance

Fórmula Haversine