Cistella elevadora

El personatge i el braç superior $ABG$ d'una plataforma elevadora mòbil de personal, coneguda com cistella elevadora tenen una massa combinada de $280 \text{ kg}$. El seu pes total actua sobre el punt $G$. Determineu les reaccions sobre el braç en el suport de passador $A$ i la magnitud de la força que el cilindre hidràulic $BC$ exerceix sobre el braç en el punt $B$.

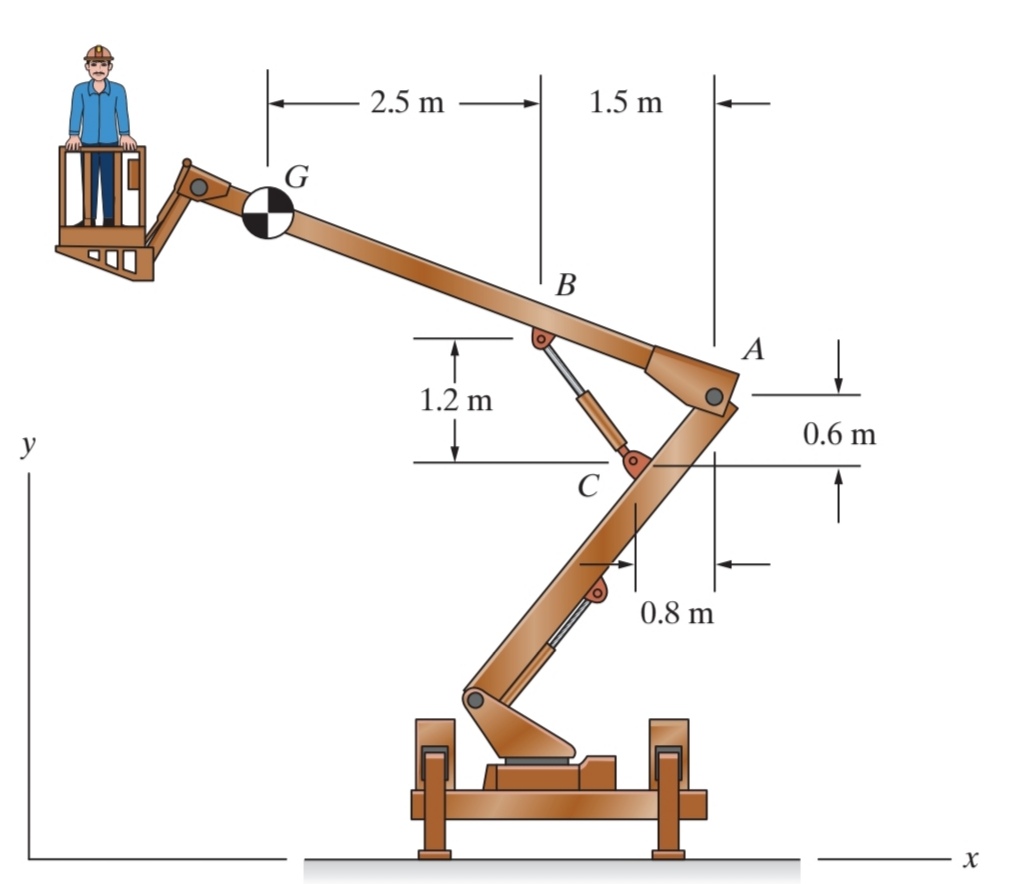
A continuació resolem l'equilibri de la grua utilitzant trigonometria directa (sinus i cosinus) i les equacions d'equilibri estàtic.

1. Dades i Geometria

Primer convertim la massa en pes (Força):

$$W = m \cdot g = 280 \text{ kg} \cdot 9,81 \text{ m/s}^2 = 2746,8 \text{ N}$$

Geometria del cilindre hidràulic ($B-C$)

Per calcular les forces, necessitem l'angle $\theta$ que forma el cilindre amb l'horitzontal. Mirem les coordenades relatives entre els punts $C$ (base) i $B$ (unió amb el braç):

Distància horitzontal ($dx$): La diferència entre 1,5m i 0,8m és $dx = 0,7 \text{ m}$.
Distància vertical ($dy$): Segons el dibuix, l'altura entre cotes és $dy = 1,2 \text{ m}$.
Longitud del cilindre ($L$): $$L = \sqrt{0,7^2 + 1,2^2} = \sqrt{1,93} \approx 1,3892 \text{ m}$$

Ara obtenim els factors trigonomètrics de l'angle $\theta$:

Cosinus (projecció horitzontal): $\cos\theta = \frac{0,7}{1,3892} \approx 0,5039$

Sinus (projecció vertical): $\sin\theta = \frac{1,2}{1,3892} \approx 0,8638$

2. Càlcul de la Força del Cilindre ($F_{BC}$)

Utilitzem l'equació de moments respecte al passador $A$ ($\sum M_A = 0$). Això és ideal perquè les reaccions a $A$ no creen moment (distància zero) i podem aïllar directament la força del cilindre.

Considerem el sentit antihorari com a positiu (+).

Desglossem els moments:

Moment del Pes ($W$):
El pes està a una distància horitzontal total de $1,5 + 2,5 = 4,0 \text{ m}$ a l'esquerra de $A$.
Gira en sentit antihorari (+).
$$M_W = + 2746,8 \cdot 4,0 = +10987,2 \text{ N}\cdot\text{m}$$
Moment de la Força Vertical del cilindre ($F_y$):
La component vertical és $F_{BC} \sin\theta$. Actua a $1,5 \text{ m}$ a l'esquerra de $A$.
Empeny cap amunt, fent girar el braç en sentit horari (-).
$$M_{Fy} = - (F_{BC} \cdot 0,8638) \cdot 1,5 = -1,2957 F_{BC}$$
Moment de la Força Horitzontal del cilindre ($F_x$):
La component horitzontal és $F_{BC} \cos\theta$. Actua a una altura sobre $A$.
L'altura del punt $B$ respecte a $A$ és $1,2 - 0,6 = 0,6 \text{ m}$.
Empeny cap a l'esquerra per sobre del pivot, creant gir antihorari (+).
$$M_{Fx} = + (F_{BC} \cdot 0,5039) \cdot 0,6 = +0,3023 F_{BC}$$

Equació final de moments:

$$10987,2 - 1,2957 F_{BC} + 0,3023 F_{BC} = 0$$ $$10987,2 - 0,9934 F_{BC} = 0$$ $$F_{BC} = \frac{10987,2}{0,9934}$$

$$F_{BC} = 11.060 \text{ N} \approx 11,06 \text{ kN}$$

3. Càlcul de les Reaccions a $A$

Ara fem servir els sumatoris de forces per trobar $A_x$ i $A_y$.

Sumatori de Forces Horitzontals ($\sum F_x = 0$)

Suposem la reacció $A_x$ cap a la dreta (+). El cilindre empeny cap a l'esquerra.

$$A_x - F_{BC} \cos\theta = 0$$ $$A_x = 11060 \cdot 0,5039$$

$$A_x \approx 5.573 \text{ N} \quad (\rightarrow)$$

Sumatori de Forces Verticals ($\sum F_y = 0$)

Suposem la reacció $A_y$ cap amunt (+).

$$A_y + F_{BC} \sin\theta - W = 0$$ $$A_y + (11060 \cdot 0,8638) - 2746,8 = 0$$ $$A_y + 9553,6 - 2746,8 = 0$$ $$A_y = 2746,8 - 9553,6$$

$$A_y = -6.807 \text{ N} \quad (\text{Cap avall } \downarrow)$$

Nota: El signe negatiu ens diu que la força realment va cap avall, contrari a la nostra suposició inicial.