Problema de la Grua Torre

Enunciat

La grua torre s'utilitza per aixecar una càrrega de 2000kg cap amunt a velocitat constant. El braç BD de 1500 kg i el braç BC de 500 kg tenen els seus centres de massa a \( G_1 \) i \( G_2 \), respectivament.

a) Determineu el moment resultant produït per la càrrega i els pesos de la grua torre respecte als punts A i B.

b) Determineu la massa necessària del contrapès C perquè el moment resultant produït per la càrrega i el pes de la grua torre respecte al punt A sigui zero. El centre de massa del contrapès es troba en \( G_3 \).

c) Determineu també la càrrega màxima que pot aixecar la grua torre a diferents distàncies des del punt B (12 m i 19 m), considerant que el contrapes té una massa de 4970 kg i que el sistema ha de mantenir-se en equilibri estàtic.

Solució

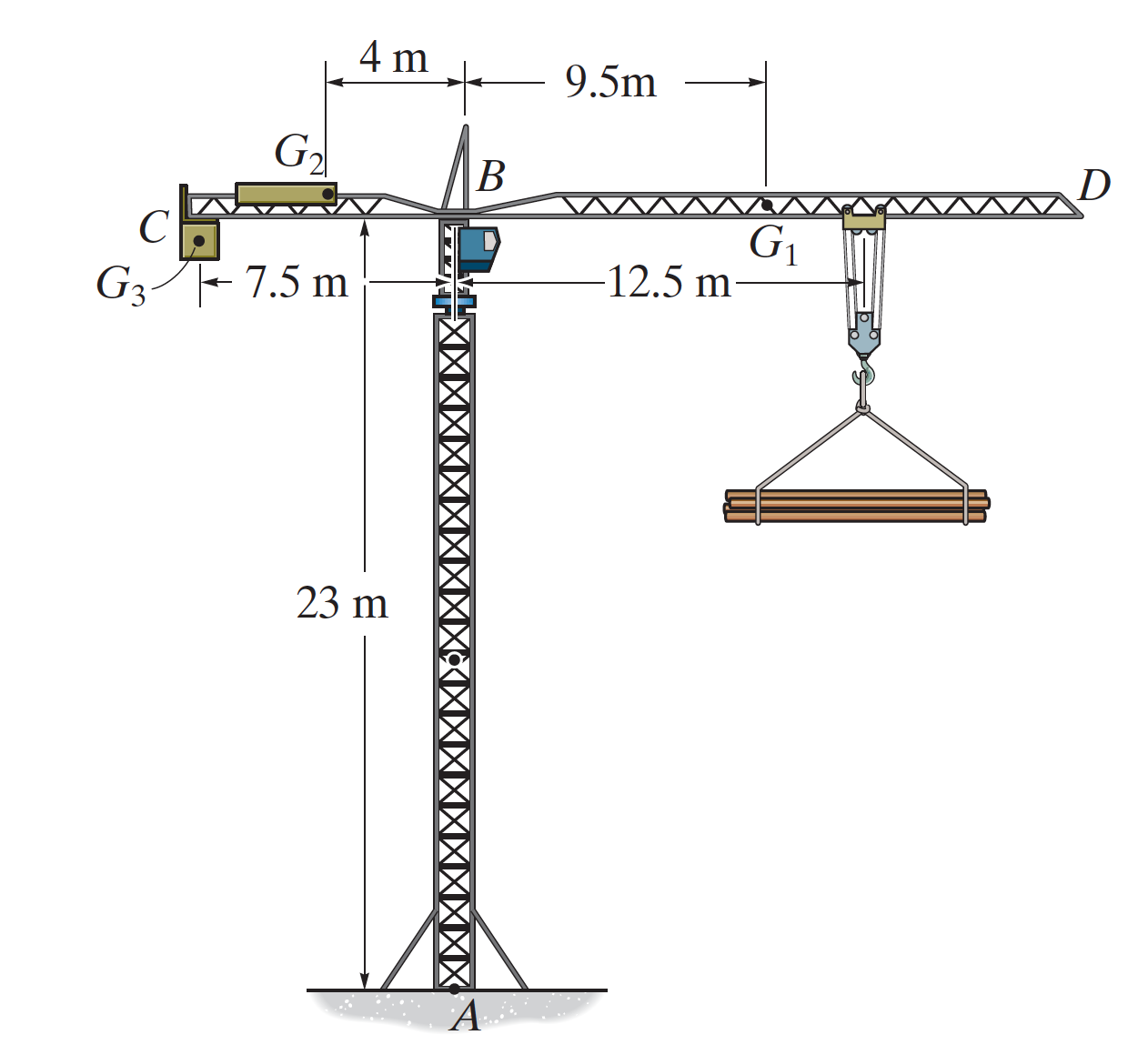
Atès que els braços de moment dels pesos i la càrrega mesurats respecte als punts A i B són els mateixos, els moments resultants produïts per la càrrega i el pes respecte als punts A i B són iguals:

a) Càlcul dels moments

Moment resultant respecte a A i B:

\[ (M_R)_A = (M_R)_B = \sum Fd \]

\[ (M_R)_A = (M_R)_B = -2000(9.81)(12.5) + 6000(9.81)(7.5) + 500(9.81)(4) - 1500(9.81)(9.5) \]

\[ = 76.0 \text{ kN·m} \]

Es discutible si el moment total ha de tenir en compte el pes de la grua A perquè la distància és zero. En canvi si considerem que existeixen reaccions i altres forces externes té sentit 76kNm que es la correció oficial del problema en la 15a. edició del famós llibre d'Enginyeria Mecànica: Estàtica de Hibbeler

He considerat correcte també la solució sense pes A de la grua que dona -365kNm

b) Càlcul de la massa del contrapès

Per tal que el moment resultant sigui zero:

\[ 0 = M_C (9.81)(7.5) + 500(9.81)(4) - 1500(9.81)(9.5) - 2000(9.81)(12.5) \]

Resolent per \( M_C \):

\[ M_C = \frac{ 1500(9.81)(9.5) + 2000(9.81)(12.5) - 500(9.81)(4) }{9.81 \times 7.5} \]

\[ M_C = 4970 \text{ kg} \]

Resposta: \( M_C = 4966.67 \) kg

c) Càlcul de la càrrega màxima \( L_{\max} \)

Plantegem l'equació d'equilibri de moments respecte a A per determinar la càrrega variable \( L \) que, aplicada a una certa distància, fa que el moment total sigui zero.

Per una càrrega situada a 12,5 m:

Els moments són:

• Càrrega variable, L: \(\displaystyle M_L = -L \cdot 9.81 \cdot 12.5\).
• Braç BD: \(\displaystyle M_{BD} = -1500 \cdot 9.81 \cdot 9.5\).
• Braç BC: \(\displaystyle M_{BC} = +500 \cdot 9.81 \cdot 4\).
• Contrapès C: \(\displaystyle M_C = +4970 \cdot 9.81 \cdot 7.5\).

L'equació d'equilibri és:
\[ 4970\cdot 9.81\cdot 7.5 + 500\cdot 9.81\cdot 4 - 1500\cdot 9.81\cdot 9.5 - L_{\max}\cdot 9.81\cdot 12.5 = 0. \]

Cancel·lant el factor \( 9.81 \):
\[ 4970\cdot 7.5 + 500\cdot 4 - 1500\cdot 9.5 - L_{\max}\cdot 12.5 = 0. \]

Calculem:

• \(4970 \cdot 7.5 \approx 37275\) kg·m.
• \(500 \cdot 4 = 2000\) kg·m.
• \(1500 \cdot 9.5 = 14250\) kg·m.

La suma dels termes coneguts:
\(37275 + 2000 - 14250 = 25025\) kg·m.

L'equació queda:
\[ 25025 - 12.5\,L_{\max} = 0 \quad\Longrightarrow\quad L_{\max} = \frac{25025}{12.5} \approx 2002 \text{ kg}. \]

Per una càrrega situada a 19 m:

Els moments de la càrrega variable seran:
\(\displaystyle M_L = -L\cdot 9.81\cdot 19\).

Plantegem l'equació d'equilibri:
\[ 4970\cdot 7.5 + 500\cdot 4 - 1500\cdot 9.5 - L\cdot 19 = 0. \]

Ja hem calculat que:
\(4970\cdot 7.5 + 500\cdot 4 - 1500\cdot 9.5 = 25025\) kg·m.

Per tant:
\[ 25025 - 19\,L = 0 \quad\Longrightarrow\quad L = \frac{25025}{19} \approx 1317 \text{ kg}. \]

Resum de resultats amb contrapès de 4970 kg:

• Moment resultant respecte a A i B: pràcticament zero (aprox. 0,15 kN·m), indicant equilibri.
• Massa del contrapès per equilibri: \( \approx 4970 \) kg.
• Càrrega màxima a 12,5 m: \( \approx 2002 \) kg.
• Càrrega màxima a 19 m: \( \approx 1317 \) kg.

Problema de la Grua

Enunciat

Una grua aixeca una càrrega L de 400 kg. El braç principal AB té una massa de 1200 kg amb centre de massa a G₁, mentre que el braç secundari BC té una massa de 600 kg amb centre de massa a G₂.

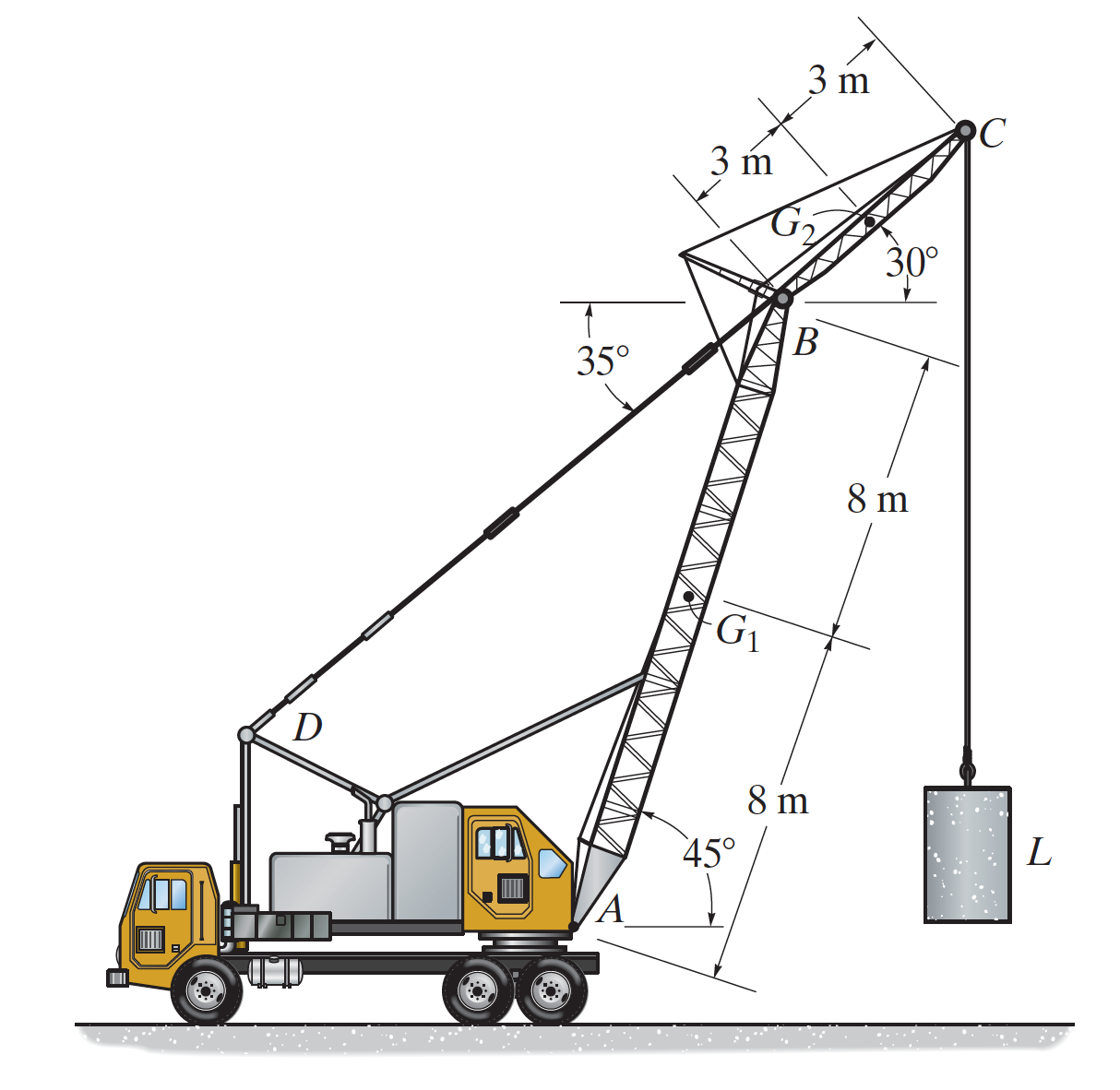
Es mostren les següents dimensions i angles:

• Distància vertical des del pern o cargol A fins a G₁: 8 m.
• Distància addicional al braç secundari (a partir de B): 3 m.
• Altres distàncies (per càlculs de moments): 16 m (distància efectiva per aplicar els pesos) i altres segments de 3 m o 6 m segons el braç.
• Angle del braç principal: 45°.
• Angle del braç secundari: 30°.
• Angle del cable BD: 35°.

Es demana determinar:

• a) La tensió en el cable BD, \( T_{BD} \).
• b) Les components horitzontals, \( A_x \), i verticals, \( A_y \), de la reacció en el pern o cargol A.
• c) Calcula el mòdul, direcció i sentit de la reacció A

Solució

a) Equilibri de Moments respecte a A

Considerant que el sistema està en equilibri rotacional, s'aplica la condició:

\[ T_{BD}\cos(35^\circ)\,(16\sin45^\circ) - T_{BD}\sin(35^\circ)\,(16\cos45^\circ) - 1200\,(9.81)(8\cos45^\circ) - 600\,(9.81)\Bigl(16\cos45^\circ+3\cos30^\circ\Bigr) - 400\,(9.81)\Bigl(16\cos45^\circ+6\cos30^\circ\Bigr)=0 \]

Despejant \( T_{BD} \) en aquesta equació, s'obté:

\[ T_{BD} \approx 76.8\,\text{kN} \]

b) Equilibri de Forces Verticals (\(\sum F_y = 0\))

Es planteja la suma de forces en la direcció vertical:

\[ A_y - T_{BD}\sin(35^\circ) - 1200\,(9.81) - 600\,(9.81) - 400\,(9.81)=0 \]

Resolent per \( A_y \):

\[ A_y \approx 65.6\,\text{kN} \]

b) Equilibri de Forces Horitzontals (\(\sum F_x = 0\))

La suma de forces en la direcció horitzontal dona:

\[ A_x - T_{BD}\cos(35^\circ)=0 \]

Per tant, la reacció horitzontal és:

\[ A_x \approx 62.9\,\text{kN} \]

Per determinar la reacció A, primer s'obté el mòdul a partir de les components horitzontal \(A_x\) i vertical \(A_y\):

\[ A = \sqrt{A_x^2 + A_y^2} = \sqrt{(62.9)^2 + (65.6)^2} \approx 90.9\,\text{kN} \]

L'angle \(\alpha\) que forma la reacció A amb l'eix horitzontal es determina amb la tangenta:

\[ \alpha = \arctan\left(\frac{A_y}{A_x}\right) = \arctan\left(\frac{65.6}{62.9}\right) \approx 46.2^\circ \]

El sentit de la reacció A és el de les components trobades: actua cap a la dreta (horitzontal) i cap amunt (vertical), equilibrant les forces i moments aplicats al sistema.

Nota: Les distàncies utilitzades en els moments (com 16 m, 8 m, 3 m, 6 m, etc.) corresponen a les distàncies efectives sobre les quals actuen els pesos dels diferents components, tal com s'ha establert en el problema original.

Problema del Carregador de Pala

Enunciat

Es vol determinar la força generada als cilindres hidràulics EF i AD per mantenir la pala en equilibri. La càrrega de la pala té una massa de 1250 kg amb centre de gravetat a G. Tots els enllaços es consideren articulats.

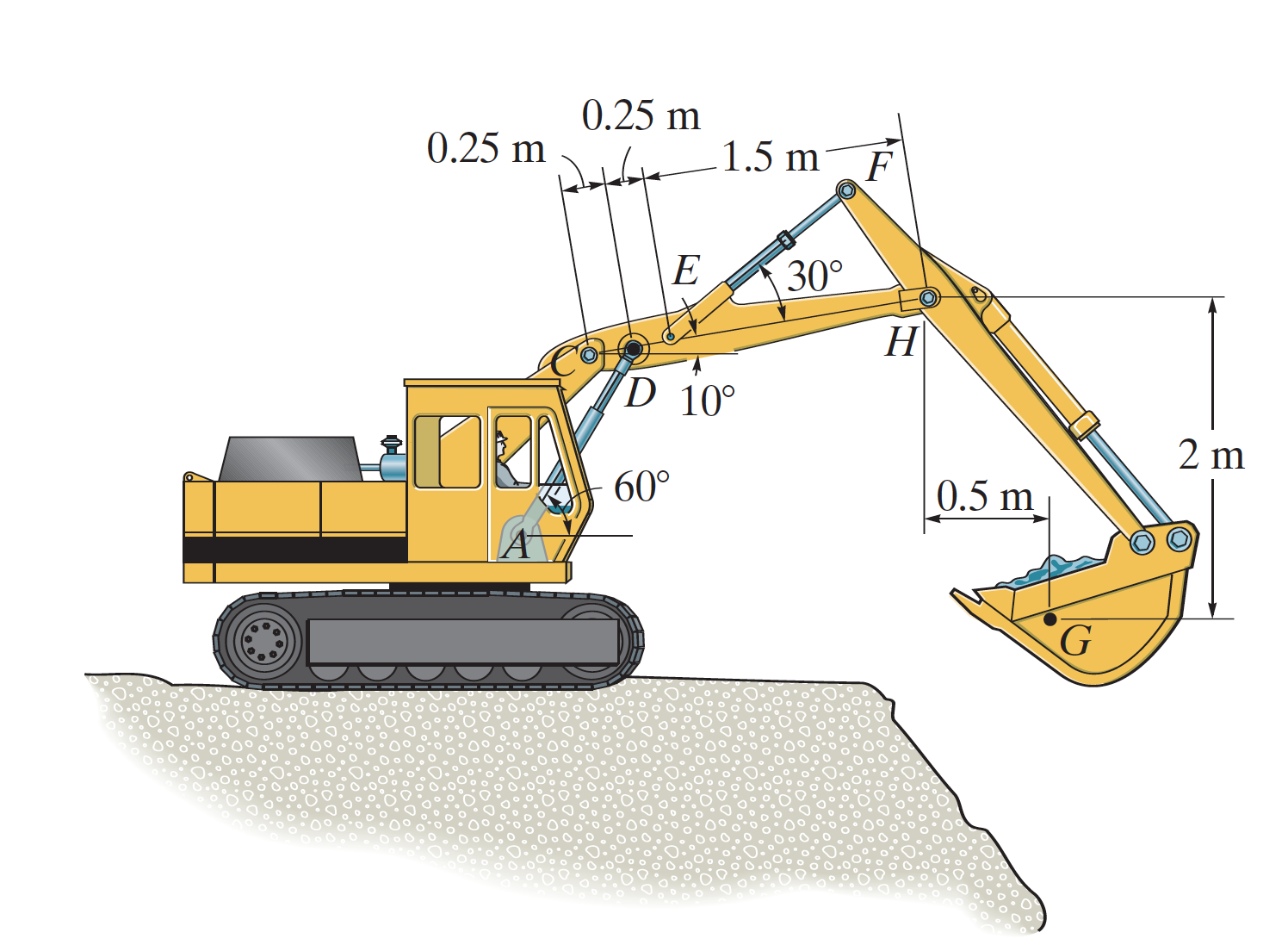
Es demana determinar:

1. La força al cilindre AD, anomenada \( F_{AD} \).
2. La força al cilindre EF, anomenada \( F_{EF} \).

Solució

1. Equilibri en l'assemblatge que inclou el punt C, E, F, H i G

Aplicant el moment al voltant del punt C (o un altre punt d'aplicació que permeti obtenir \( F_{AD} \)), tenim:

\[ F_{AD}\cos(40^\circ)(0.25) - 1250\,(9.81)\Bigl(2\cos(10^\circ)+0.5\Bigr)=0 \]

Despejant \( F_{AD} \):

\[ F_{AD} = \frac{1250\,(9.81)\Bigl(2\cos(10^\circ)+0.5\Bigr)}{0.25\cos(40^\circ)} \approx 1.58\times10^5\,\text{N} = 158\,\text{kN} \]

2. Equilibri en l'assemblatge que inclou els punts F, E, i G

Prenent moments al voltant del punt H, on actua \( F_{EF} \), tenim:

\[ -1250\,(9.81)(0.5) + F_{EF}\,(1.5\sin30^\circ)=0 \]

Resolent per \( F_{EF} \):

\[ F_{EF} = \frac{1250\,(9.81)(0.5)}{1.5\sin30^\circ} \approx 8.18\times10^3\,\text{N} = 8.18\,\text{kN} \]

Resum de resultats:

• \( F_{AD} \approx 158\,\text{kN} \)
• \( F_{EF} \approx 8.18\,\text{kN} \)

Nota: Els càlculs es basen en les condicions d'equilibri (tant de forces com de moments) per a un sistema amb enllaços articulats, tenint en compte els efectes dels pesos i les distàncies proporcionades.