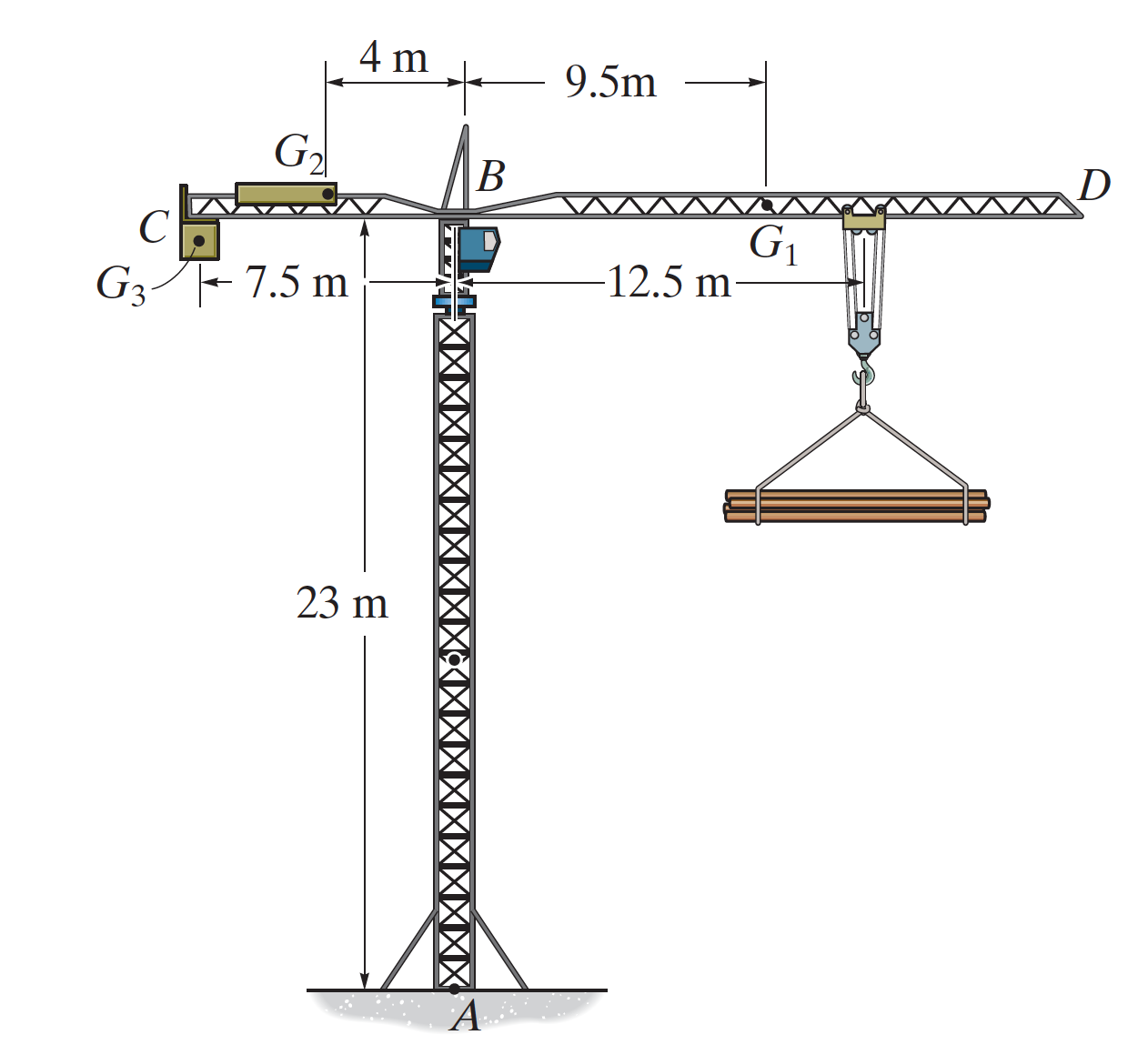
La grua torre s'utilitza per aixecar una càrrega de 2000 kg cap amunt a velocitat constant. El braç BD de 1500 kg i el braç BC de 500 kg tenen els seus centres de massa a \( G_1 \) i \( G_2 \), respectivament.
a) Determineu el moment resultant produït per la càrrega i els pesos de la grua torre respecte als punts A i B.
b) Determineu la massa necessària del contrapès C perquè el moment resultant produït per la càrrega i el pes de la grua torre respecte al punt A sigui zero. (Comprovarem que es necessita un contrapès de 4970 kg.)
c) Determineu també la càrrega màxima que pot aixecar la grua torre a diferents distàncies des del punt B, considerant que el contrapès té una massa de 4970 kg i que el sistema ha de mantenir-se en equilibri estàtic. Aquest càlcul es realitzarà per una càrrega situada a 12 m (en lloc de 12,5 m).
Recorda que el moment d’una força respecte a un punt es calcula com el producte de la força pel braç (distància perpendicular respecte al punt considerat). Els signes indiquen si el moment té tendència a fer la rotació en sentit horari o antihorari.
Utilitzem els següents valors:
La suma dels moments respecte al punt A (o B) es pot expressar com: \[ (M_R)_A = (M_R)_B = -2000\,(9.81)(12.5) + 4970\,(9.81)(7.5) + 500\,(9.81)(4) - 1500\,(9.81)(9.5). \]
Discussió sobre quan incloure el moment respecte a A:
En alguns casos, pot resultar útil calcular els moments respecte a diferents punts de rotació (A o B) per verificar l’equilibri global del sistema.
Si el punt d’aplicació de les forces està ben definit, el càlcul respecte a A pot donar més informació sobre com es distribueixen els moments.
Per aquest problema, els moments calculats respecte a A o B condueixen al mateix resultat d’equilibri, sempre que es mantingui la coherència en la definició dels braços de palanca.
Per tal que el moment resultant respecte a A sigui zero, plantegem l'equació: \[ 0 = +4970\,(9.81)(7.5) + 500\,(9.81)(4) - 1500\,(9.81)(9.5) - 2000\,(9.81)(12.5). \]
Cancel·lant el factor comú \(9.81\) i resolent per la massa del contrapès \(M_C\), obtenim: \[ M_C = \frac{1500\,(9.5) + 2000\,(12.5) - 500\,(4)}{7.5} \approx 4970 \text{ kg}. \]
Aquesta massa de 4970 kg és la que s'utilitza per assegurar que el sistema estigui en equilibri momentànic respecte al punt A.
Per determinar la càrrega variable \( L \) que, aplicada a 12 m des del punt B, fa que el moment total sigui zero, plantegem l’equació d’equilibri de moments respecte a A:
Els moments són:
L’equació d’equilibri queda: \[ 4970\,(9.81)(7.5) + 500\,(9.81)(4) - 1500\,(9.81)(9.5) - L_{\max}\,(9.81)(12) = 0. \]
Cancel·lant el factor \(9.81\): \[ 4970\cdot 7.5 + 500\cdot 4 - 1500\cdot 9.5 - 12\,L_{\max} = 0. \]
Calculem els termes coneguts:
La suma és: \[ 37275 + 2000 - 14250 = 25025 \text{ kg·m}. \]
L'equació final per a \( L_{\max} \) és: \[ 25025 - 12\,L_{\max} = 0 \quad\Longrightarrow\quad L_{\max} = \frac{25025}{12} \approx 2085 \text{ kg}. \]
Aquest enfocament mostra que la posició on s'aplica la càrrega (12 m vs. 12,5 m) té un impacte directe sobre la càrrega màxima que es pot aixecar, i que la discussió sobre el punt de càlcul (A o B) pot variar segons el context del problema i la interpretació dels braços de palanca.