Problema de la Grua Torre

Enunciat

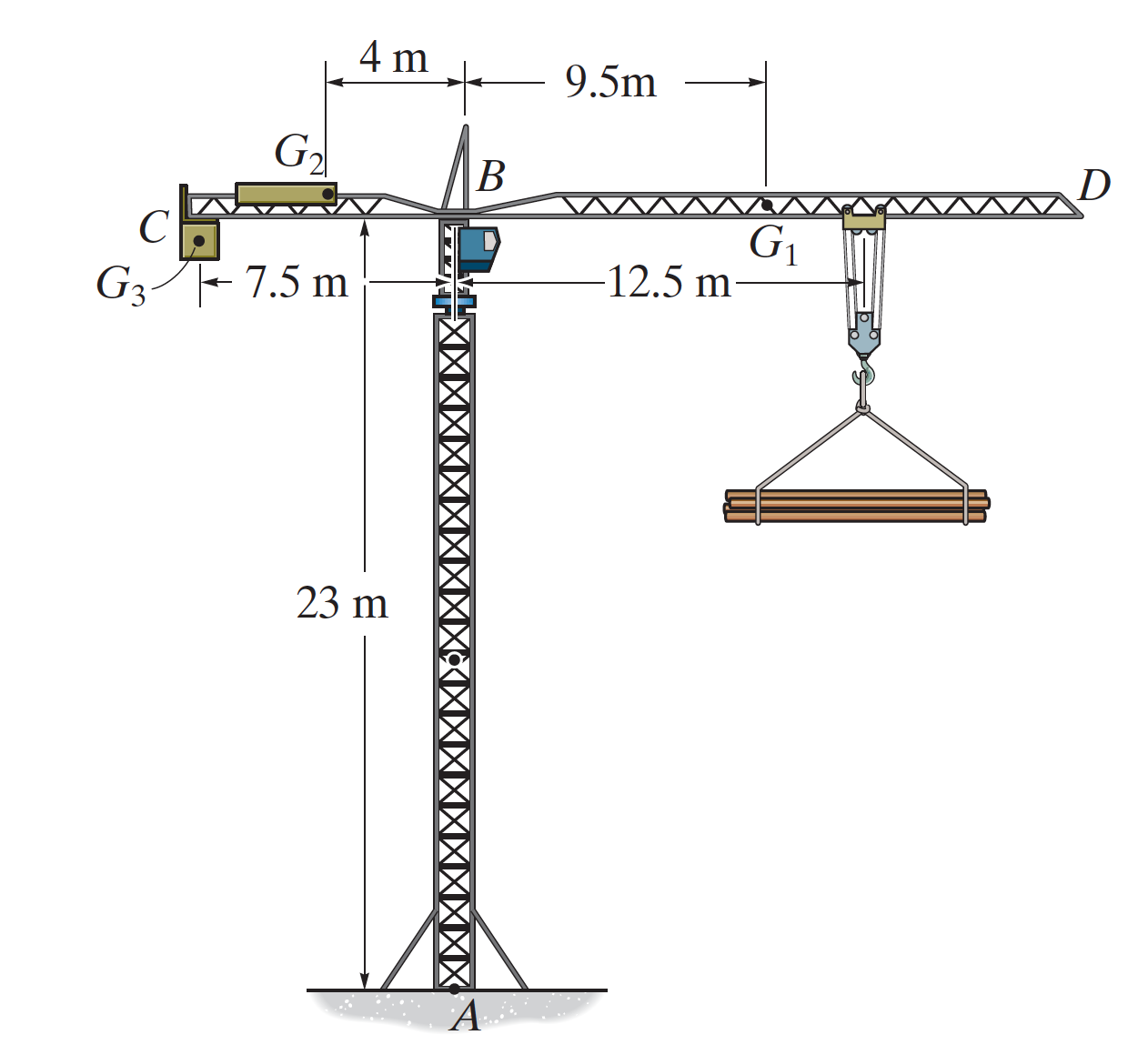
La grua torre s'utilitza per aixecar una càrrega de 2000 kg cap amunt a velocitat constant. El braç BD de 1500 kg i el braç BC de 500 kg tenen els seus centres de massa a \( G_1 \) i \( G_2 \), respectivament.

a) Determineu el moment resultant produït per la càrrega i els pesos de la grua torre respecte als punts A i B.

b) Determineu la massa necessària del contrapès C perquè el moment resultant produït per la càrrega i el pes de la grua torre respecte al punt A sigui zero. (En aquest cas, comprovarem que es necessita un contrapès de 4970 kg.)

c) Determineu també la càrrega màxima que pot aixecar la grua torre a diferents distàncies des del punt B (12,5 m i 19 m), considerant que el contrapès té una massa de 4970 kg i que el sistema ha de mantenir-se en equilibri estàtic.

Solució

Recorda que el moment d’una força respecte a un punt es calcula com el producte de la força pel braç (distància perpendicular respecte al punt considerat). Els signes indiquen si el moment té tendència a fer la rotació en sentit horari o antihorari.

a) Càlcul dels moments respecte a A i B

Utilitzem els següents valors:

• Càrrega L: 2000 kg, braç de 12,5 m (moment negatiu): \(\displaystyle M_L = -2000 \cdot 9.81 \cdot 12.5\).
• Braç BD: 1500 kg, braç de 9,5 m (moment negatiu): \(\displaystyle M_{BD} = -1500 \cdot 9.81 \cdot 9.5\).
• Braç BC: 500 kg, braç de 4 m (moment positiu): \(\displaystyle M_{BC} = +500 \cdot 9.81 \cdot 4\).
• Contrapès C: 4970 kg, braç de 7,5 m (moment positiu): \(\displaystyle M_C = +4970 \cdot 9.81 \cdot 7.5\).

La suma dels moments és:
\[ (M_R)_A = (M_R)_B = -2000(9.81)(12.5) + 4970(9.81)(7.5) + 500(9.81)(4) - 1500(9.81)(9.5). \]

Fent els càlculs:

• \(2000 \cdot 12.5 = 25000\); \(\;25000 \cdot 9.81 \approx 245250\) N·m.
• \(4970 \cdot 7.5 \approx 37275\); \(\;37275 \cdot 9.81 \approx 365572\) N·m.
• \(500 \cdot 4 = 2000\); \(\;2000 \cdot 9.81 \approx 19620\) N·m.
• \(1500 \cdot 9.5 = 14250\); \(\;14250 \cdot 9.81 \approx 139793\) N·m.

Sumem tenint en compte els signes:
\( -245250 + 365572 + 19620 - 139793 \approx 149.5 \) N·m.

Així, amb un contrapès de 4970 kg el moment resultant és gairebé zero (aproximadament 0,15 kN·m), cosa que indica que el sistema es troba gairebé en equilibri.

b) Càlcul de la massa del contrapès

Per tal que el moment resultant respecte a A sigui zero, plantegem:
\[ 0 = M_C (9.81)(7.5) + 500(9.81)(4) - 1500(9.81)(9.5) - 2000(9.81)(12.5). \]

Resolent per \( M_C \):
\[ M_C = \frac{1500(9.81)(9.5) + 2000(9.81)(12.5) - 500(9.81)(4)}{9.81 \cdot 7.5}. \]

Fent els càlculs (com s'ha vist en els punts anteriors) s'obté aproximadament:
\[ M_C \approx 4970 \text{ kg}. \]

Aquesta massa és la que hem emprat en els càlculs de la part (a), i verifica l'equilibri momentànic.

c) Càlcul de la càrrega màxima \( L_{\max} \)

Plantegem l'equació d'equilibri de moments respecte a A per determinar la càrrega variable \( L \) que, aplicada a una certa distància, fa que el moment total sigui zero.

Per una càrrega situada a 12,5 m:

Els moments són:

• Càrrega variable, L: \(\displaystyle M_L = -L \cdot 9.81 \cdot 12.5\).
• Braç BD: \(\displaystyle M_{BD} = -1500 \cdot 9.81 \cdot 9.5\).
• Braç BC: \(\displaystyle M_{BC} = +500 \cdot 9.81 \cdot 4\).
• Contrapès C (actualitzat): \(\displaystyle M_C = +4970 \cdot 9.81 \cdot 7.5\).

L'equació d'equilibri és:
\[ 4970\cdot 9.81\cdot 7.5 + 500\cdot 9.81\cdot 4 - 1500\cdot 9.81\cdot 9.5 - L_{\max}\cdot 9.81\cdot 12.5 = 0. \]

Cancel·lant el factor \( 9.81 \):
\[ 4970\cdot 7.5 + 500\cdot 4 - 1500\cdot 9.5 - L_{\max}\cdot 12.5 = 0. \]

Calculem:

• \(4970 \cdot 7.5 \approx 37275\) kg·m.
• \(500 \cdot 4 = 2000\) kg·m.
• \(1500 \cdot 9.5 = 14250\) kg·m.

La suma dels termes coneguts:
\(37275 + 2000 - 14250 = 25025\) kg·m.

L'equació queda:
\[ 25025 - 12.5\,L_{\max} = 0 \quad\Longrightarrow\quad L_{\max} = \frac{25025}{12.5} \approx 2002 \text{ kg}. \]

Per una càrrega situada a 19 m:

Els moments de la càrrega variable seran:
\(\displaystyle M_L = -L\cdot 9.81\cdot 19\).

Plantegem l'equació d'equilibri:
\[ 4970\cdot 7.5 + 500\cdot 4 - 1500\cdot 9.5 - L\cdot 19 = 0. \]

Ja hem calculat que:
\(4970\cdot 7.5 + 500\cdot 4 - 1500\cdot 9.5 = 25025\) kg·m.

Per tant:
\[ 25025 - 19\,L = 0 \quad\Longrightarrow\quad L = \frac{25025}{19} \approx 1317 \text{ kg}. \]

Resum de resultats amb contrapès de 4970 kg:

• Moment resultant respecte a A i B: pràcticament zero (aprox. 0,15 kN·m), indicant equilibri.
• Massa del contrapès per equilibri: \( \approx 4970 \) kg.
• Càrrega màxima a 12,5 m: \( \approx 2002 \) kg.
• Càrrega màxima a 19 m: \( \approx 1317 \) kg.