Problema de navegació — Tarifa → Ceuta
0) Conversió de coordenades (DMS → decimal)
Per treballar amb fórmules trigonomètriques, necessitem les coordenades en decimal. A continuació convertim pas a pas.
Tarifa
| Latitud (DMS) | 36° 0′ 45″ N |
|---|
| Longitud (DMS) | 5° 36′ 20.16″ W |
|---|
Per convertir a decimal: $$Lat = 36 + \frac{0}{60} + \frac{45}{3600} = 36.0125^\circ$$
I la longitud: $$Lon = -(5 + \frac{36}{60} + \frac{20.16}{3600}) = -5.6056^\circ$$
Ceuta
| Latitud (DMS) | 35° 53′ 17.88″ N |
|---|
| Longitud (DMS) | 5° 18′ 56.16″ W |
|---|
Latitud en decimal: $$Lat = 35 + \frac{53}{60} + \frac{17.88}{3600} = 35.8883^\circ$$
Longitud en decimal: $$Lon = -(5 + \frac{18}{60} + \frac{56.16}{3600}) = -5.3156^\circ$$
1) Diferències angulars
Calcularem la diferència de latitud i longitud per després aplicar Haversine:
$$\Delta \varphi = Lat_{Ceuta} - Lat_{Tarifa} = -0.1242^\circ$$
$$\Delta \lambda = Lon_{Ceuta} - Lon_{Tarifa} = 0.2900^\circ$$
Convertim a radians, ja que trigonometria utilitza radians:
$$\Delta \varphi_{rad} = -0.1242 \times \frac{\pi}{180} = -0.002166\ rad$$
$$\Delta \lambda_{rad} = 0.2900 \times \frac{\pi}{180} = 0.005061\ rad$$
2) Distància amb Haversine
Haversine permet calcular distància sobre la superfície esfèrica de la Terra:
$$a = \sin^2\left(\frac{\Delta \varphi}{2}\right) + \cos(Lat_{Tarifa} \frac{\pi}{180}) \cos(Lat_{Ceuta} \frac{\pi}{180}) \sin^2\left(\frac{\Delta \lambda}{2}\right)$$
$$a \approx 3.39 \times 10^{-6}$$
$$c = 2 \arcsin(\sqrt{a}) \approx 0.003567\ rad$$
Convertim a milles nàutiques: $$d_{NM} = \frac{6371 \cdot c}{1.852} \approx 15.945\ NM$$
3) Rumb inicial
El rumb indica la direcció inicial cap a Ceuta:
$$y = \sin(\Delta \lambda_{rad}) \cos(Lat_{Ceuta} \frac{\pi}{180}) \approx 0.0041$$
$$x = \cos(Lat_{Tarifa} \frac{\pi}{180}) \sin(Lat_{Ceuta} \frac{\pi}{180}) - \sin(Lat_{Tarifa} \frac{\pi}{180}) \cos(Lat_{Ceuta} \frac{\pi}{180}) \cos(\Delta \lambda_{rad}) \approx 0.0019$$
$$\theta = \arctan2(y,x) \approx 117.79^\circ$$
4) Aproximació plana
Per veure-ho de manera geomètrica simple:
Component Nord-Sud: $$NS = |\Delta Lat| \times 60 = 0.1242 \times 60 = 7.45\ NM$$
Analitzant longitud vs latitud
Un grau de latitud és constant a tota la Terra i representa aproximadament 60 milles nàutiques (111 km) entre paral·lels, perquè les línies de latitud són paral·leles i equidistants. En canvi, un grau de longitud varia amb la latitud. A l’equador, un grau de longitud també correspon a unes 60 milles nàutiques, però a mesura que ens acostem als pols, la distància entre dos meridians consecutius disminueix, ja que les línies de longitud convergeixen cap als pols, fins a trobar-se a zero a l’extrem nord i sud. Per calcular la distància real corresponent a un canvi de longitud en qualsevol latitud, hem de multiplicar la diferència de longitud per el factor \(\cos(lat\_mitjana)\). Així, encara que la diferència angular sigui la mateixa, la distància sobre la superfície terrestre depèn de la latitud, fent que un grau de longitud no sigui equivalent a un grau de latitud fora de l’equador. Aquesta correcció és essencial per obtenir distàncies precises quan es navega o es fa cartografia.
Longitud a lat mitjana: $$1^\circ lon = 60 \cos(35.95^\circ) \approx 49.2\ NM$$
Component Est-Oest: $$EW = \Delta Lon \times 49.2 = 0.2900 \times 49.2 \approx 14.27\ NM$$
Distància total: $$d = \sqrt{NS^2 + EW^2} \approx 16.1\ NM$$
5) Temps de travessia
Temps = distància / velocitat:
$$t = \frac{d_{NM}}{V} = \frac{15.945}{6} = 2.6575\ h$$
Convertim hores decimals a h:m:s pas a pas:
Hores: $$H = \lfloor 2.6575 \rfloor = 2h$$
Minuts decimals: $$(2.6575-2) \times 60 = 39.45m$$
Minuts sencers: $$M = \lfloor 39.45 \rfloor = 39m$$
Segons: $$(39.45-39) \times 60 = 27s$$
Temps final: $$t = 2h\;39m\;27s$$
Hora d'arribada: $$09:42:54 + 2:39:27 = 12:22:21$$
6) Consum i cost de combustible
Consum total: $$Q = 18 \times 2.6575 \approx 47.84\ L$$
Cost: $$Cost = 47.84 \times 1.425 \approx 68.17\ \text{€}$$
7) Vector de velocitat, corrent i vent (detall pas a pas)
Per calcular la trajectòria real de la nau, hem de combinar el vector de velocitat de la nau amb els vectors de corrent i vent. Ho fem en components cartesianes (Est = u, Nord = v) amb cada rumb.
Formules generals
$$u = s \sin\theta, \quad v = s \cos\theta$$
On $s$ és la velocitat del vector i $\theta$ el rumb en graus.
Pas 1: Nau
Velocitat de la nau $s = 6\ kn$, rumb $\theta = 117.8°$:
Calcul del component Est (u):
$$u_{nau} = 6 \times \sin(117.8°) \approx 5.31$$
Calcul del component Nord (v):
$$v_{nau} = 6 \times \cos(117.8°) \approx -2.80$$
Pas 2: Corrent
Velocitat de la corrent $s = 1.5\ kn$, rumb $\theta = 120°$:
$$u_{corrent} = 1.5 \times \sin(120°) \approx 1.30$$
$$v_{corrent} = 1.5 \times \cos(120°) \approx -0.75$$
Pas 3: Vent
Velocitat del vent $s = 12\ kn$, rumb $\theta = 150°$:
$$u_{vent} = 12 \times \sin(150°) \approx 6.00$$
$$v_{vent} = 12 \times \cos(150°) \approx -10.39$$
Pas 4: Suma de vectors
Sumem component a component per obtenir el vector resultant:
Component Est (u):
$$u_{res} = u_{nau} + u_{corrent} + u_{vent} = 5.31 + 1.30 + 6.00 \approx 12.61$$
Component Nord (v):
$$v_{res} = v_{nau} + v_{corrent} + v_{vent} = -2.80 - 0.75 - 10.39 \approx -13.94$$
Pas 5: Magnitud i rumb del resultant
Magnitud del vector resultant (velocitat efectiva):
$$S = \sqrt{u_{res}^2 + v_{res}^2} = \sqrt{12.61^2 + (-13.94)^2} \approx 18.8\ kn$$
Rumb del vector resultant:
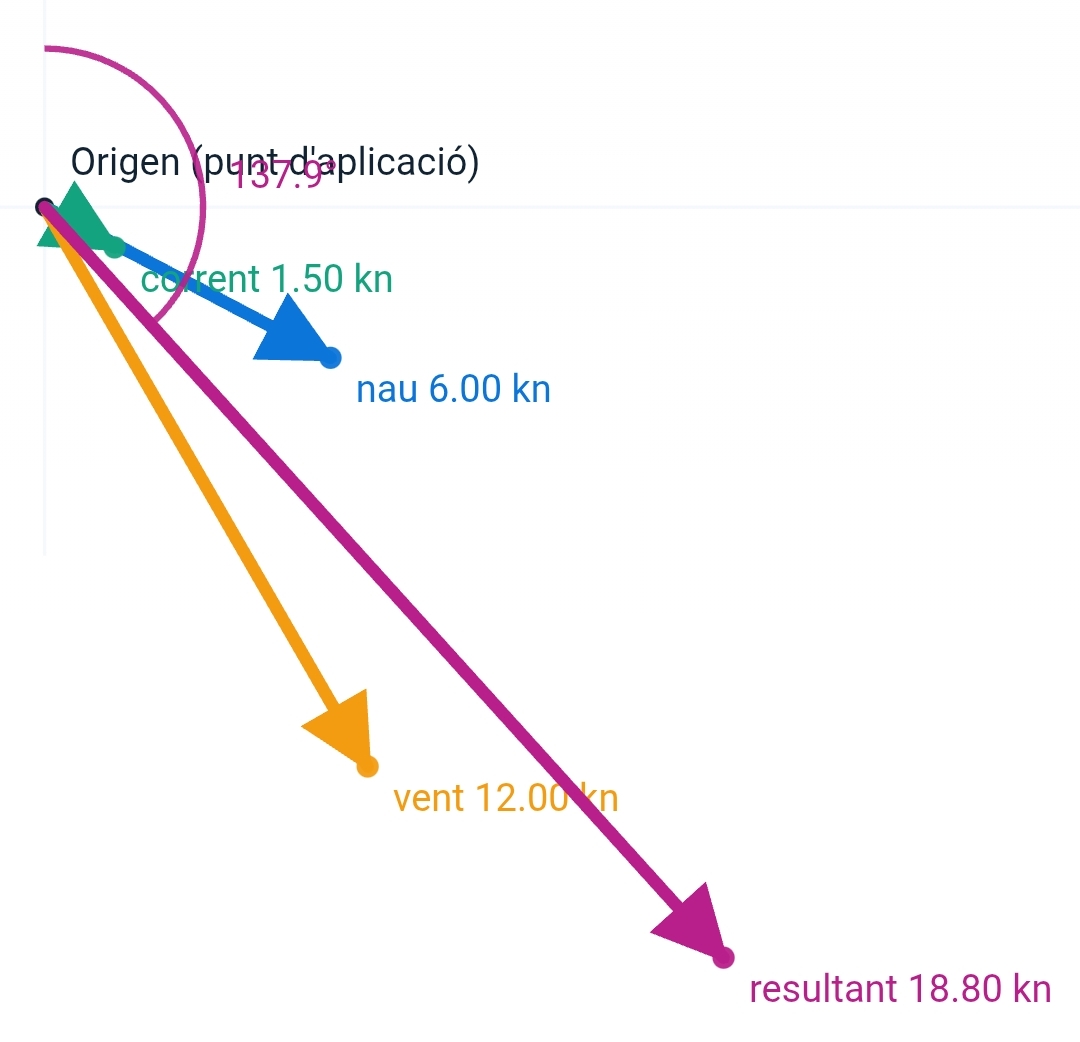
$$\theta = \arctan2(u_{res}, v_{res}) = \arctan2(12.61, -13.94) \approx 137.9°$$
Aquesta magnitud i rumb representen la trajectòria i velocitat real de la nau tenint en compte la influència del vent i la corrent, pas essencial per la navegació precisa.
8) Resum final
- Distància: 15.945 NM
- Rumb: 117.8°
- Temps: 2h 39m 27s
- Arribada: 12:22:21
- Consum: 47.84 L
- Cost: 68.17 €
